頑張る中学生を応援するかめきち先生です。
今回は
「相似な図形」の分野を
勉強していると出てくる、
三角形と平行線の線分の比
について、
お話をしていきます。
よく
高校入試や
模擬試験で出題されるところ
なので、
しっかりと押さえておきましょう!
三角形と平行線の線分の比
まずは
三角形と平行線の線分の比の
ルールを覚えましょう。
ポイントは
①2つの辺が平行であれば
②どの辺の比の関係が成り立つのか
を押さえる
というところになります。
ルールは
2つの図形のパターン
について
覚えておきましょう!
1つ目のパターン
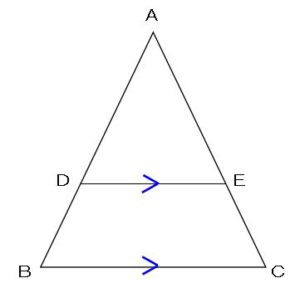
前提として
図のように
DEとBCが平行(DE//BC)
である必要があります。
(この前提を
忘れないでくださいね!)
すると
次のような
比の関係が成り立ちます。
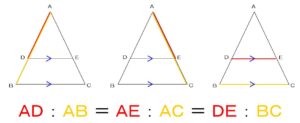
「小さい三角形△ADEと
大きな三角形△ABCの
辺を対比させる」
と覚えておくと
分かりやすいと思います。
※理由は
△ADEと△ABCは
相似の関係になるからです。
同時に
次の比の関係も
成り立ちます。
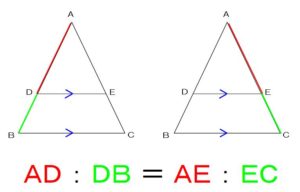
2つ目のパターン
2つ目の
図形のパターンは、
次のものです。
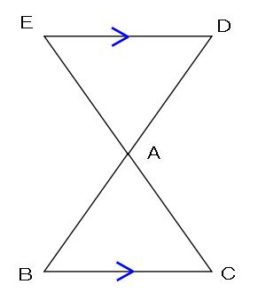
1つ目のパターンと
同じように、
前提として
DEとBCが平行(DE//BC)
である必要があります。
すると
次の比の関係が
成り立ちます。
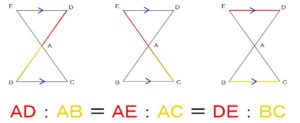
※この関係が
成り立つ理由も、
△ADEと△ABCは
相似の関係にあるからです。
同時に
次の比の関係も
成り立ちますが、
もし分かりにくければ
このパターンは
あまり出題されることは
多くないので、
前のものを
押さえておけば
大丈夫です。
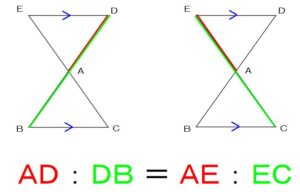
※ AB : BD = AC : CE
も成り立ちます。
三角形と平行線の線分の比のルールの逆
今度は
今までとは逆に、
線分の比から
2つの辺が
平行線であることが
言えるという
ルールも押さえておきましょう。
ポイントは
①どの辺の比の関係が成り立たてば
②2つの辺が平行である
ということになるのかを
押さえる
ということになります。
1つ目のパターン
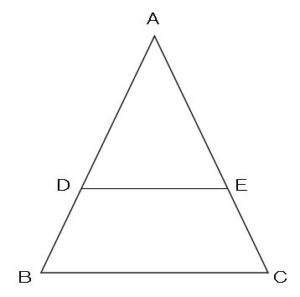
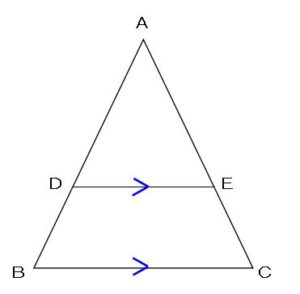
このような
三角形の図において
次の比の関係が
成り立つ場合、
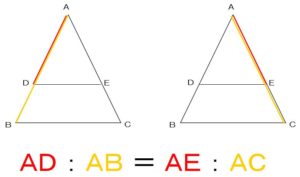
辺DEと辺BCは
平行である
ということが言えます。
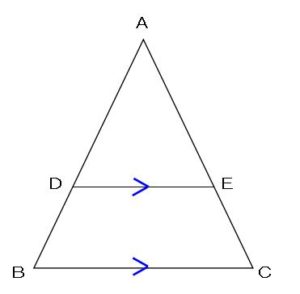
また
次の比の関係が
成り立つ場合も、
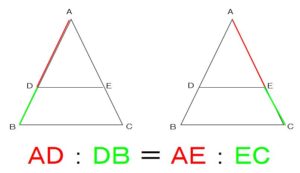
辺DEと辺BCは
平行である
ということが言えます。
2つ目のパターン
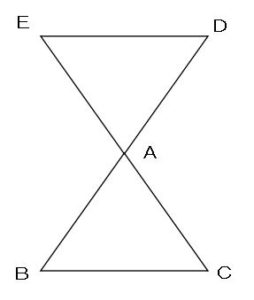
このような
図において、
次の比の関係が
成り立つ場合、
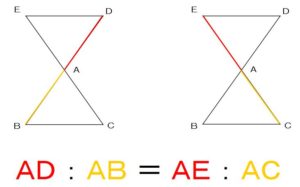
辺DEと辺BCは
平行である
ということが言えます。
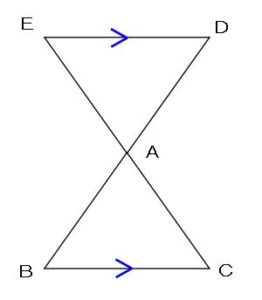
また
次の比の関係が
成り立つ場合も、
(※このケースも
覚えられればで
大丈夫です。)
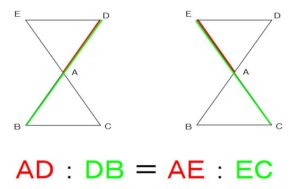
辺DEと辺BCは
平行である
ということが言えます。
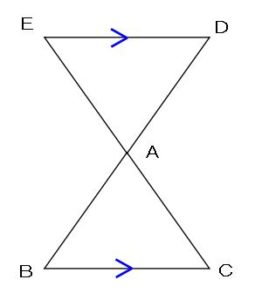
三角形と平行線の線分の比は、
今まで
ルールを説明してきたような
単純な図形として
出題されることもありますが、
複雑な図形の中から
今まで説明してきた
三角形の
図形のパターンを
自分で見つけ出して
ルールを使用する、
という形で
出題されることが
とても多いです。
演習問題に
たくさん取り組んで、
短い時間で
図形のパターンを
見つけ出して
ルールが使えるように、
練習してみて下さい。
まとめ

三角形と平行線の線分の比について
まとめます。
1.三角形と平行線の線分の比のルール
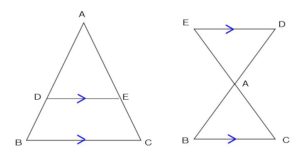
① DE//BCであれば、AD : AB = AE : AC = DE : BC
② DE//BCであれば、AD : DB = AE : EC
2.三角形と平行線の線分の比のルールの逆
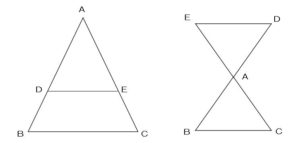
① AD : AB = AE : AC であれば、DE//BC
② AD : DB = AE : EC であれば DE//BC
頑張るあなたなら
必ずできるようになりますよ。
頑張る中学生を
かめきち先生は応援しています。
最後まで読んでいただき
ありがとうございました。