頑張る中学生を応援するかめきち先生です。
今回は
定期テストはもちろん
高校受験の時にもよく出題される
「この三角形の面積は
全体の図形の面積の
何分のいくつでしょうか?」
という問題を解くコツについて、
お話をしていきます。
今回のお話は
三角形の面積比を使用しますが、
三角形の面積比の求め方には
高さが同じ三角形の場合や
相似な三角形の場合など、
いくつかパターンがあります。
その中で
よく出題される1つの
パターンについて
お話をしていきます。
考え方を
しっかりとマスターしておけば
一見複雑そうに見える問題でも
ちゃんと対応できるようになるので、
頑張って身につけておきましょう!
基本は、高さが同じ三角形の面積比を使う
例えば
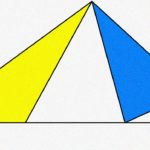
次のような図がある場合、
△APCの面積は
△ABCの面積の何倍になるか
分かるでしょうか?
※図中の数字は、辺の比を表します。
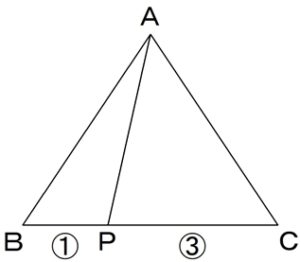
この場合は、
高さが同じ三角形の面積比は
底辺の長さの比と同じになる
という考え方を使います。
BPとPCの辺の比が
1 : 3
なので、
△ABPと△APCの面積比も
1 : 3
になります。
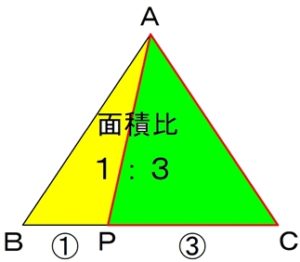
ということは
△APCに対しての
全体△ABCの面積比は、
△ABP(1)と△APC(3)の面積比を足した
「4」ということになります。
なので
全体△ABCと△APCの面積比は
4 : 3
となり、
△APC = △ABC × 3/4
ということになります。
※全体△ABCの底辺BCと
△APCの底辺PCの比を
直接比べて、
全体△ABCと△APCの面積比は
4 : 3
としても
当然かまいません。
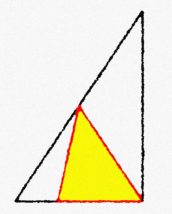
複雑な図形は、求める図形を含むブロックを残していく
それでは
次の図の場合、
△APCの面積は
△DBCの面積の何倍に
なるでしょうか?
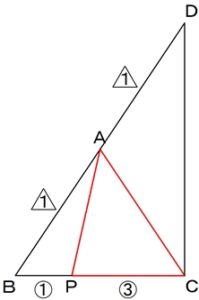
この場合も
高さが同じ三角形の面積比は
底辺の長さの比と同じになる
という考え方を使って、
△APCの面積比は
全体のいくつになるか
ということを求めていきますが、
ここで1つコツがあります。
それは
面積比を求めたい図形(△APC)を含む
ブロックを残して
三角形をどんどん切っていく
という方法を使う、
ということです。
やり方を
詳しく説明していきます。
まず
全体△DBCに注目すると、
△CADと
求めたい△APC(赤の枠線)を含む
△CABとに
分割できることが分かります。
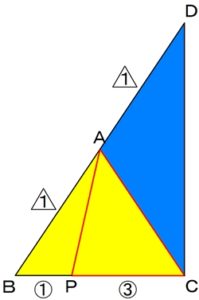
ここで
必要となるのは△APC(赤の枠線)を含む
△CABの部分(黄色)なので、
△CABのブロックが
全体△DBCの何倍になるかを
考えます。
全体△DBCと△CABの
底辺の比は
DB:AB=2:1
なので、
面積比の関係も
△DBC:△CAB=2:1となり
△CAB=△DBC×1/2 ・・・ ①
(あとで、この式をもう一度使います。)
ということを
求めることができます。

次に
残った△CABに注目して、
求めたい△APC(緑)が
△CABの何倍になるのかを
考えます。
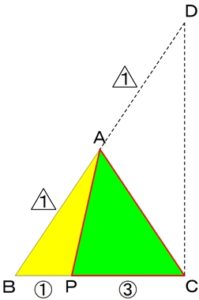
先ほどと同じように
底辺の比(BC:PC=4:3)から
△APC=△CAB×3/4 ・・・ ②
になることが分かります。
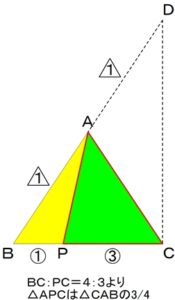
ここで最初に
△CAB=△DBC×1/2 ・・・ ①
と求めているので、
②の△CABの部分に
①の式を代入して、
△APC=△DBC×1/2×3/4
=△DBC×3/8
となり
△APCの面積は
△DBCの面積の3/8倍である
ということを求めることができます。
※考え方が分かったら
代入などせずに、
三角形を切っていくたびに
ダイレクトに全体△DBCに
1/2と3/4を
かけてしまってかまいません。
問題にチャレンジ
それでは
今までの話を踏まえて、
次の問題にチャレンジしてみて下さい。
次の図で
△GEFの面積は
△ABCの面積の
何倍になるでしょうか?
※図中の数字は、辺の比を表します。
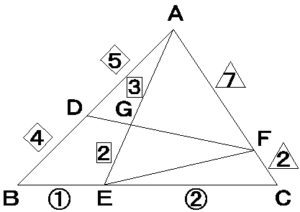
どうでしょうか?
答えを求められたでしょうか?
それでは
解き方の説明を行っていきます。
まず
全体△ABCを
面積比を求めたい△GEFを含む
△AECのブロックを残して、
三角形を次の図のように切ります。
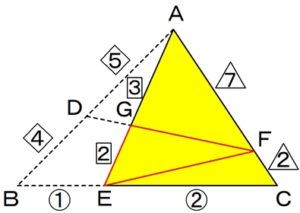
全体△ABCと△AECの
底辺の比は
BC:EC=3:2
なので、
面積比の関係も
△ABC:△AEC=3:2となり、
△AEC=△ABC×2/3 ・・・①
とあらわすことができます。
続いて
△AECを
面積比を求めたい△GEFを含む
△AEFのブロックを残して、
次の図のように切ります。
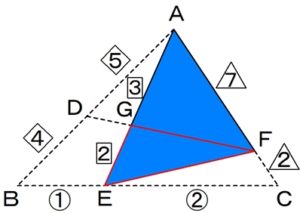
さきほどと同じように
△AECと△AEFの
底辺の比は
AC:AF=9:7
なので、
面積比の関係も
△AEC:△AEF=9:7となり、
△AEF=△AEC×7/9 ・・・②
とあらわすことができます。
最後に
△AEFを
面積比を求めたい△GEFの
ブロックを残して、
次の図のように切ります。
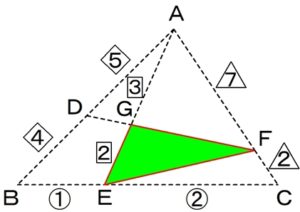
今までと同じように
△AEFと△GEFの
底辺の比は
AE:GE=5:2
なので、
面積比の関係も
△AEF:△GEF=5:2となり、
△GEF=△AEF×2/5 ・・・ ③
とあらわすことができます。
ここまで求めてきた
つぎの3つの式より
△AEC=△ABC×2/3 ・・・①
△AEF=△AEC×7/9 ・・・②
△GEF=△AEF×2/5 ・・・③
対応する三角形のところに
それぞれの式を代入していきます。
(①の式を②に代入して、
その結果を③に代入する。)
すると
△GEF=△ABC×2/3×7/9×2/5
=△ABC×28/135
となり、
△GEFの面積は
△ABCの面積の
28/135倍である
と答えを求めることができます。
まとめ

三角形が全体の図形の中に
組み込まれていて、
その三角形と全体の図形の
面積比(「全体の図形の何倍か?」)を
求める問題を解くコツについて
まとめます。
1.「高さが同じ三角形の面積比は
底辺の長さの比と同じになる」
という考え方を利用する。
2.三角形が複雑な図形の中に
組み込まれている場合は、
面積比を求めたい三角形を含む
ブロックを残して
図形をどんどん切っていく。
あきらめずにねばり強くやりつづけることで
必ずできるようになります!
頑張る中学生をかめきち先生は応援しています。
最後まで読んでいただき
ありがとうございました。