頑張る中学生を応援するかめきち先生です。
突然ですが例題です。
(例題)
連続する3つの整数の和が3の倍数になることを
文字を使って説明しなさい。
・
・
・
どうですか。
「連続する3つの整数の文字式」が
頭に浮かびましたか?
このような
整数や自然数について聞いてくる
文章題を解くときに
ポイントになるのが、
質問されている内容の
整数や自然数を文字を使った式で
あらわすことができるか
ということになります。
この例題の場合だと
「連続する3つの整数」を
n-1、n、n+1 (nは整数)
と文字を使って
考えることができましたか
ということになります。
文章で聞かれている内容を
きちんと文字の式であらわすことができれば、
50%は問題を解けてしまったと
言ってもいいと思います。
「整数や自然数についての文章題」は
よく出されるパターンが決まっているので、
それらをおさえてしまえば
この分野の問題は大丈夫です。
今回は
よく出される
「文字を使った整数や自然数のあらわし方」について
お話をしていきます。
よく出される6つのパターンについて
マスターしてしまいましょう!
連続する3つの整数
最初は「連続する3つの整数」についてです。
例えば、「3、4、5」などですね。
「n」を整数とすると
「n-1、n、n+1」
とあらわすことができます。
※「n、n+1、n+2」でも
もちろん合っていますが、
まん中の数を「n」にしておくと
その後の計算が楽になることが多いので
覚えておきましょう!
ここで大事なのが、
「n」を整数とする
という断りをいれておく
ということです。
「n」が何をあらわしているのか
宣言しておかないと、
少数を入れてもOKということに
なってしまいますからね。
証明問題で
「整数や自然数について
文字を使った式」であらわす
必要がある場合は、
「n」が何をあらわしているのか
証明文の中で宣言することを
忘れないようにしてください。
3つの連続した偶数
続いて「3つの連続した偶数」についてです。
例えば、「4、6、8」などが
「3つの連続した偶数」になりますよね。
偶数は必ず「2で割ることができる」
という性質があります。
なので
「n」を整数として
偶数をあらわす場合は、
「2n」
とあらわすことができます。
では「3つの連続した偶数」は
どのようにあらわすのでしょうか?
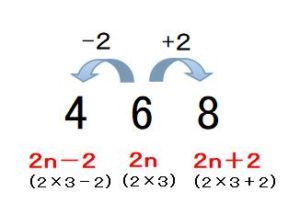
偶数は2ずつはなれているので、
「2n-2、2n、2n+2」
とあらわすことができます。
実際に数字を入れて確認してみて下さい。
3つの連続した奇数
それでは次に
「3つの連続した奇数」の
あらわし方です。
例えば、「3、5、7」などが
そうですね。
「n-2、n、n+2」
でよさそうな気がするけれども、
nに4を入れると、
「2、4、6」となって
連続する3つの偶数となってしまうので
ちがいますね。
実は奇数の性質は
「偶数より1大きい」
ということが言えます。
なので奇数は
「偶数+1」
とあらわすことができます。
偶数は先ほど「2n」と
あらわすことができたので、
「n」を整数として
奇数をあらわす場合は、
「2n+1」
とあらわします。
では「3つの連続した奇数」は
どのようにあらわすのかというと、
偶数と同じように2ずつはなれているので
下の図のようになります。

奇数は2ずつはなれているので、
「2n-1、2n+1、2n+3」
とあらわすことができます。
2桁の自然数
続いて「2桁の自然数」のあらわし方です。
よく証明問題で
一の位と十の位を入れかえた数についての
問題が出されたりします。
例えば
「23」
という数字の場合を考えてみましょう。
十の位の数をa
一の位の数をb
とします。

「a+b」であらわせそうですが、
実際に
aに2
bに3
を入れて計算をしてみると、
「2+3=5」となり
「23」とはなりませんね。
2桁の自然数を文字であらわす場合は、
十の位の数には10倍
一の位の数は1倍
してあげるのが正解です。
実際にやってみると
「2×10+3×1」となり
「23」になります。
2桁の自然数を
十の位をa
一の位をb
として式であらわす場合は、
「10a+b」
となります。
●の倍数
それでは次に5の倍数など
「●の倍数」のあらわし方についてです。
これはけっこう分かりやすいのでは
ないかと思います。
例えば5の倍数であれば
必ず5で割ることができますね。
「5、10、15」などが
そうですよね。
別の言い方をすると
5に何か整数をかけた数字に
必ずなります。
5の倍数は
「n」を整数とすると
「5n」
とあらわすことができます。
なので
「●の倍数」を
「n」を整数としてあらわす場合は、
「●n(=●×n)」
となります。
■で割って▲あまる数
最後に
3で割って1あまる数など
「■で割って▲あまる数」の
あらわし方についてです。
例えば
3で割って1あまる数は
「4、7、10」などが
あります。
これらの数は
別の言い方をすると、
「3の倍数に1をたしたもの」
ということができます。
4は「3(3の倍数)+1」
7は「6(3の倍数)+1」
10は「9(3の倍数)+1」
となりますよね。
ということは
3の倍数は
「n」を整数とすると
「3n」とあらわすことができるので、
3で割って1あまる数は
「3n+1」
とあらわすことができます。
「■で割って▲あまる数」を
「n」を整数としてあらわす場合は、
「■n(=■×n)+▲」
となります。
実際に例を使ってチェックしてみよう
最後に
「整数や自然数を文字であらわす式」を
考えるときに、
やってもらいたいことがあります。
それは
実際に数字を入れてみて
式が正しいかチェックしてみる
ということです。
どのように式を組み立ててよいか
分からなくなってしまった場合も、
実際に数字を使って
式を考えてみると、
式を思い出したり
組み立てることができたり
することがとても多いです。
なので
質問されている内容に合った
実際の簡単な数字を使って、
式をチェックしたり考えるということを
必ず行うようにしてください。
まとめ

よく出される
「文字を使った整数や自然数のあらわし方」
の6パターンのまとめです。
1.連続する3つの整数
「n」を整数とすると
「n-1、n、n+1」
2.3つの連続した偶数
「n」を整数とすると
「2n-2、2n、2n+2」
3.3つの連続した奇数
「n」を整数とすると
「2n-1、2n+1、2n+3」
4.2桁の自然数
十の位をa
一の位をb
とすると
「10a+b」
5.●の倍数
「n」を整数とすると
5の倍数は
「5n」
6.■で割って▲あまる数
「n」を整数とすると
3で割って1あまる数は
「3n+1」
あなたなら、やれば必ずできるようになります。
頑張る中学生をかめきち先生は応援しています。
最後まで読んでいただきありがとうございました。