頑張る中学生を応援するかめきち先生です。
今回は
連立方程式の文章題としてよく出題される
「2けた自然数」の問題を解くコツについて、
お話をしていきます。
「2けたの自然数」を文字を使って
どのように表すのか、
考え方をしっかりと理解しておけば
高校入試などで出題される
複雑なものにも対応できるようになるので、
ここでしっかりとポイントを
おさえておきましょう!
ポイントは2つ
まずは例題です。
2けたの自然数があり、十の位は一の位の2倍より1小さい。
また、十の位の数字と一の位の数字を入れかえてできる数は、
もとの数より9小さい。
もとの数を求めなさい。
このような問題が出題された場合、
ポイントとなるのは
次の2点です。
ポイント1
各けたの数字を
文字を使って表す。
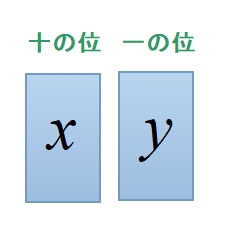
十の位の数字をx
一の位の数字をy
で表す。
ポイント2
2ケタの自然数を
文字を使って式で表す。
もとの数
10x+y
十の位の数字と一の位の数字を入れかえてできる数
10y+x
それぞれのポイントについて
説明をしていきます。
ポイント1:各けたの数字を文字を使って表す
これは十の位、一の位
2けたのそれぞれの数字を
文字のxとyを使って
表すということです。
例えば、
十の位をx
一の位をy
で表すとした場合、
もとの自然数が「62」であれば
x=6
y=2
ということになります。
ここで注意しなければいけないのは、
xとyは各けたの数字を意味しているだけで
足してももとの自然数にはならない
ということです。
xとyを足しても「6+2=8」になるだけで
「62」にはなりませんよね。
注意してください。
ポイント2:2けたの自然数を式を使って表す
これは
2ケタの自然数(もとの数、十の位の数字と一の位の数字を入れかえてできる数)を
先ほどのxとyを使って
式で表すということです。
結論から言うと
2けたの自然数(もとの数)の場合は、
十の位をx
一の位をy
としたのであれば、
2けたの自然数(もとの数)=10×x+1×y
で表すことができます。
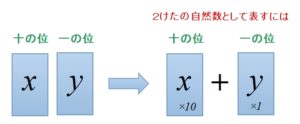
なぜそのようになるのかというと、
十の位のx
一の位のy
はそれぞれの位の数字を表しているだけなので、
2けたの自然数として表すには
十の位のxには10をかけて
一の位のyには1をかけて
両方をたす
ということを行う必要があります。
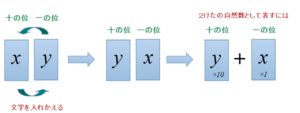
同じような考え方で
十の位の数字と一の位の数字を入れかえてできる数を
式で表す場合は、
2けたの自然数(十の位の数字と一の位の数字を入れかえてできる数)
=10×y+1×x
と表すことができます。
※もし3けたの自然数を
百の位をx
十の位をy
一の位をz
として各位を文字で表すのであれば、
3けたの自然数は
100×x+10×y+1×z
という式で表すことができます。
例題を解いてみよう
それでは
これまでにお話をした
2つのポイントを使って、
例題を解いていきましょう。
(例題)
2けたの自然数があり、十の位は一の位の2倍より1小さい。
また、十の位の数字と一の位の数字を入れかえてできる数は、
もとの数より9小さい。
もとの数を求めなさい。
まずは
1つ目のポイントでお話をした
「各けたの数字を文字を使って表す」
ということを行います。
2けたの自然数の
十の位を「x」
一の位を「y」
と表します。

問題文に
「十の位は一の位の2倍より1小さい」とあるので、
x(十の位の数字)=2×y(一の位の数字)-1 ・・・①
という式を作ることができます。
※この式はあとで使います。
続いて
2つ目のポイントでお話をした
「2けたの自然数を式を使って表す」
ということを行っていきます。
もとの数の2ケタの自然数と
十の位の数字と一の位の数字を入れかえてできる数
を次のように表します。
2けたの自然数(もとの数)=10×x+1×y
2けたの自然数(十の位の数字と一の位の数字を入れかえてできる数)
=10×y+1×x
そして問題文に
「十の位の数字と一の位の数字を入れかえてできる数は、
もとの数より9小さい」
とあるので、
これをそのまま式に書きかえると
(十の位の数字と一の位の数字を入れかえてできる数)=(もとの数)-9
10×y+1×x=(10×x+1×y)-9・・・②
という式を作ることができます。
ここまでで
xとyを使った
①と②の2つの異なる式ができたので、
この2つの式の連立方程式を解いて
xとyを求めていきます。
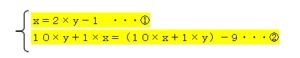
この連立方程式を解くと
x=3
y=2
となります。
ということで
もとの数は「32」であるということを
求めることができます。
どうでしょうか?
2ケタの自然数を求める問題で、
「十の位の数字と一の位の数字を入れかえてできる数」などと
問題文に出てきたら、
2つのポイントをしっかりと思い出して
取り組んでみて下さい。
まとめ

連立方程式の文章題
「2けたの自然数」の問題を解くコツについて
まとめます。
1.各けたの数字を
文字を使って表す。
(十の位の数字をx
一の位の数字をy
で表す。)
2.2ケタの自然数(もとの数、十の位の数字と一の位の数字を入れかえてできる数)を
xとyを使って式で表す。
2けたの自然数(もとの数)=10×x+1×y
2けたの自然数(十の位の数字と一の位の数字を入れかえてできる数)
=10×y+1×x
あなたなら、分かるまでねばり強く頑張り続けることができますよ。
頑張る中学生をかめきち先生は応援しています。
最後まで読んでいただき
ありがとうございました。