頑張る中学生を応援するかめきち先生です。
今回は
複雑な計算を行っているときに、
「これを移項するにはどうやるんだろう?」
と迷ってしまうときに
使えるコツについてお話していきます。
次のような計算問題が出題されました。
あなたならどのように解きますか?

やり方は、
h以外のものを
すべて=(イコール)の逆側に移項して、
最終的に h= の形になるように
なおしてあげればいいんですよね。
移項をスムーズに行えるのであれば、
これから説明することは
特に意識しなくて当然大丈夫です。
ただ計算の途中で、
「これはどうやって移項すればいいんだろう?」
と計算が止まってしまう時は
次のように考えてみるといいですよ。
=(イコール)の式の4つの性質
実際に計算を行ってみる前に
「=(イコール)の式の性質」について
確認しておきます。
「=(イコール)の式」は、
次のような計算を行っても
=(イコール)の関係は崩れないよ、
という性質があります。
もとの式が、下の式だとすると
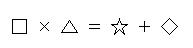
①両辺に同じ数をたす
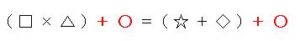
②両辺から同じ数をひく
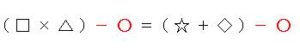
③両辺に同じ数をかける
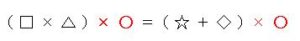
④両辺を同じ数でわる
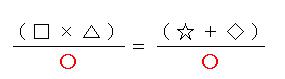
この4つの性質を使って
移項を行っていきます。
ポイントは、じゃま者を消していく!
それでは実際に
計算を行っていきます。
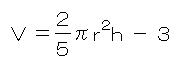
「hについて解きなさい」という問題なので
hだけ片側に残して、
あとは全部=(イコール)の逆側に
移動(=移項)してあげればいいですよね。
ここでポイントは
h以外のじゃま者(移項したいもの)を
1つずつ消していく
ということです。
hは=(イコール)の右側にあるので、
右側にhだけ残るように
他のものを1つずつ消していくことを
考えていきます。
ここで消す順番にルールが1つだけあります。
+(プラス)や-(マイナス)の
固まり(項)のじゃま者があれば
先にそれを消して、
その後に
残したい文字(この場合はh)に
かけられたり(×)、
残したい文字をわっている(÷)じゃま者を
消していきます。
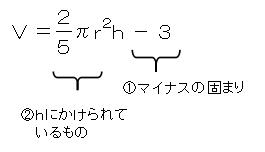
まず最初のじゃま者は
「-3」です。
「-3」を消すには
3を+(プラス)して0(ゼロ)にして
しまえばいいですが、
右側だけ3を+(プラス)してしまうと
=(イコール)が成り立たなく
なってしまうので、
左側も3を+(プラス)します。
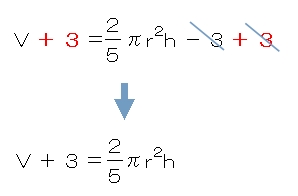
さて、次はどのじゃま者を消していきますか?
hにかけられているものの
どれを選択してもよいですが、
今回は「2/5(5分の2)」を消していきましょう。
「2/5(5分の2)」を消すには
逆数の5/2(2分の5)をかけて、
結果が1になるようにしてあげればいいですよね。
この場合も、
=(イコール)の関係が崩れないように
両辺に5/2(2分の5)をかけてあげます。
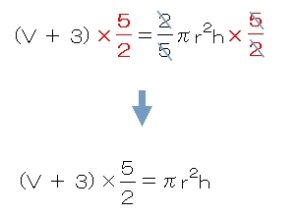
次はじゃま者の「π」を消していきましょう。
「π」を消すには、
やはり逆数の1/π(π分の1)をかけて
結果が1になるようにしてあげればいいですよね。
=(イコール)の関係が崩れないように
両辺に1/π(π分の1)をかけていきます。
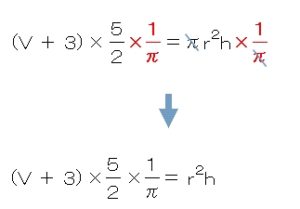
さあ、残すじゃま者は「r2」だけになりました。
「r2」だと消し方が変わるのかなと
思うのかもしれないけれども、
やり方は同じです。
「r2」の逆数である1/r2(r2分の1)を
両辺にかけていきます。
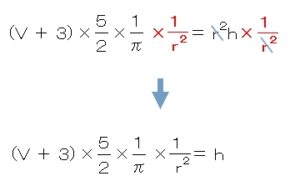
さあ、これで=(イコール)の右側は
hだけになりました。
左側は、×(かける)の記号が付いたまままので
記号をなくした形に書きなおします。
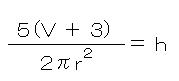
最後に
=(イコール)の左側と右側を入れかえても
関係は変わらないので、
左右を入れかえてh=の形にします。
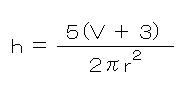
これが答えです。
どうでしょうか。
両辺から同じ数をひいたり、
両辺に消したい数字や文字の
逆数をかけたりなどして、
じゃま者を消していく。
移項の仕組みを「見える化」して
計算をしているのですが、
このやり方だと
間違えずに移項して
計算を進めることができると思いますよ。
まとめ

移項のやり方に迷った時のコツについて
まとめます。
1.じゃま者(移項したいもの)を1つずつ
消していくことを考えていく
2.じゃま者(移行したいもの)を消す順番は、
+(プラス)や-(マイナス)の
固まり(項)のじゃま者があれば
先にそれを消して、その後に
残したい文字にかけられたり(×)、
残したい文字をわっている(÷)じゃま者を
消していく。
3.消し方は、
=(イコール)をはさんだ両辺に
同じものをたす(+)
同じものをひく(-)
同じものをかける(×)
同じもので割る(÷)
の4つの方法のどれかを使って
じゃま者を消していく。
途中であきらめないで、分かるまでねばっていこう!
頑張る中学生をかめきち先生は応援しています。
最後まで読んでいただきありがとうございました。