頑張る中学生を応援するかめきち先生です。
今回は
平面図形の分野で
定期テストや高校受験でよく出題される
「図形の中にある
2つの三角形の面積を比べる問題を解くコツ」
についてお話していきます。
考え方のコツさえつかめば
色々な出題パターンにも対応できるようになるので、
是非マスターしておきましょう!
基準にできる図形を探すこと
さて
いきなりですが問題です。
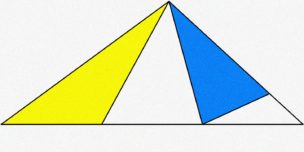
下の図で
△ABDの面積は
△AEFの面積の何倍になるでしょうか?
※図中の数字は辺の比を表します。
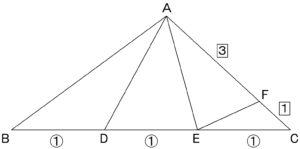
2つの三角形が相似の関係や
頂点が同一で高さが同じ三角形であれば
直接面積を比べることができますが、
そうでない場合は
どのようにすればよいのでしょうか?
このように
直接2つの図形を比べることができない場合は、
2つの三角形それぞれからみて
基準にできる共通な図形を探してみます。
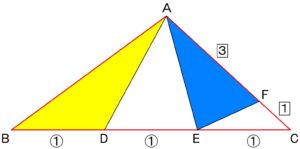
なにを言っているのかというと、
この問題の場合
全体の△ABCに注目してみると、
△ABDの面積は△ABCの面積の何倍か
ということは求められそうです。
また
△AEFの面積についても
△ABCの面積の何倍か
ということが求められそうです。
このように
△ABDと△AEFは、
全体の△ABCを基準として
それぞれ△ABCの面積の何倍か
ということを考えることによって、
面積を比較することができるようになります。
それでは
実際に問題を解いていきます。
ABDの面積を求める
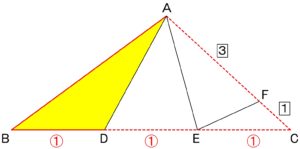
△ABDに注目すると
全体の△ABCと
頂点Aを共通にする高さが同じ三角形になるので、
BD : BC = 1:3 より
△ABDの面積 = △ABCの面積 × 1/3 ・・・ ①
と求めることができます。
△AEFの面積を求める
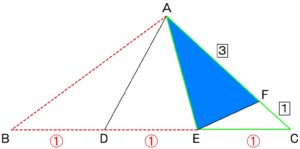
つづいて
△AEFに注目すると、
一度に求められそうにないので
まずは△AECの面積が
全体の△ABCの何倍かということを
考えます。
EC : BC = 1:3 より
△AECの面積 = △ABCの面積 × 1/3 ・・・ ②
と求めることができます。
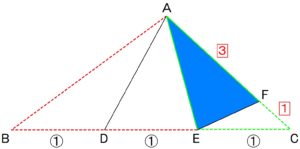
つづいて
△AEFの面積が
△AECの面積の何倍かということを考えます。
△AEFは
△AECと頂点Eを共通にする高さが同じ三角形になるので、
AC : AF = 4:3 より
△AEFの面積 = △AECの面積 × 3/4 ・・・ ③
となります。
ここで先ほど求めた②の結果より、
△AECの面積が全体の△ABCの面積の何倍か
ということが分かっているので、
それを今求めた③に代入すると
△AEFの面積 = △ABCの面積 × 1/3 × 3/4
= △ABCの面積 × 1/4 ・・・ ④
となります。
△ABDと△AEFの面積を比べる
ここで一旦整理すると
①の結果より
△ABDの面積 = △ABCの面積 × 1/3 ・・・ ①
④の結果より
△AEFの面積 = △ABCの面積 × 1/4 ・・・ ④
ということになります。
よって
△ABDと△AEFの面積の比は、
△ABCの面積 × 1/3 : △ABCの面積 × 1/4 = 4 : 3
ということになります。
問題は
△ABDの面積は
△AEFの面積の何倍になるでしょうか?
と聞いているので、
答えは 「4/3(3分の4)倍」になります。
どうでしょうか?
図形を直接比べられない場合は、
基準にできる図形を探すというコツを思い出して
是非問題にチャレンジしてみて下さい。
まとめ

図形の中にある
2つの三角形の面積を
比べる問題を解くコツについて
まとめます。
1.2つの三角形の面積を
直接比べられない場合は、
それぞれの三角形を含む
共通の図形などを探して、
それぞれの三角形が
基準となる図形の面積の何倍か
ということを考えることによって
面積を比べることができる。
「分かろう」とねばり強く続けていれば必ず身につきますよ。
頑張る中学生をかめきち先生は応援しています。
最後まで読んでいただき
ありがとうございました。