頑張る中学生を応援するかめきち先生です。
今回は
ニガテとしている生徒が多い
「数学の文章題を解くためのコツ その2」について
お話をしていきたいと思います。
以前にアップした
「数学。文章題が苦手な君へ。文章題を解くコツ!」
の記事では、
一次方程式や
連立方程式の文章題を
解くときに、
文章題に書かれている内容を
しっかりと理解することが
できれば、
自分の力で式を組み立てて
問題を解ける生徒が多い
というお話をしました。
そして
文章題の内容を
しっかりと理解するためには、
文章に書かれている内容を
整理して分かりやすくするとよく、
具体的な方法として
「文章に書かれている内容を
図にしてみる」
というやり方を
紹介しました。
今回は
「文章に書かれている内容を
図にしてみる」
ということにプラスして、
意識してこの方法を使って
文章を整理してみると、
文章が何を言っているのか
理解しやすくなる
という方法について
お話をしていきたいと思います。
文章を短く区切って、1つ1つ理解していく!
(問題)
あるお店に、定価が1個60円のグッズAが120個と、1個80円のグッズB100個がありました。
最初に定価で両方とも販売したところ、グッズAはグッズBより10個少なく売れました。
両方とも売れ残りが出たので、残りをすべて定価の30%引きで販売したところ、グッズAは5個売れ残り、グッズBはすべて売れました。
最初に販売したものと、割引後に販売したもののすべての売上金額の合計は、13610円になりました。
最初に定価で販売した時に売れた、グッズAの個数とグッズBの個数を求めなさい。
このような問題が
出題されました。
あなたなら
どのように解いていきますか?
この問題文の文章を
一気に理解しようとすると、
頭がこんがらがって
しまいますよね。
そこで
このような長い文章題に
取り組むときには、
一気に分かろうとしないで
文章を短く区切って
1つ1つていねいに
内容を整理して、
最後にまとめて
理解するようにすると
よいです。
それでは
実際に文章を短く区切って
1つ1つ見ていこうと
思います。
まず
最初の部分です。
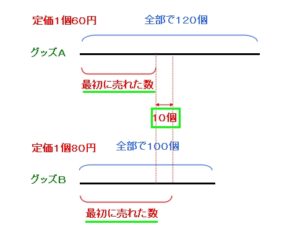
①「あるお店に、定価が1個60円のグッズAが120個と、1個80円のグッズB100個がありました。」
図を使って整理すると
こういうことですね。
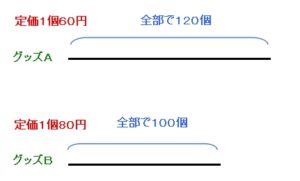
②「最初に定価で両方とも販売したところ、グッズAはグッズBより10個少なく売れました。」
ここから分かることは
グッズAは1個60円の定価で、
グッズBは1個80円の定価で、
販売したということですね。
そして両方とも
何個売れたかは
分からないけれども、
グッズAの方が
グッズBより
10個少なく売れた
ということが分かります。
図を使って整理すると
こういうことですよね。
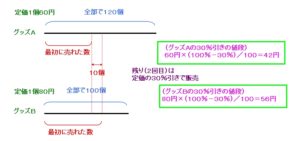
③「両方とも売れ残りが出たので、残りをすべて定価の30%引きで販売したところ、」
だんだん内容が
複雑になってきたので、
分かるところで
いったん区切ってしまいます。
ここから分かることは
両方とも売れ残っているので、
グッズAは残りを
定価の30%引きで、
グッズBも残りを
定価の30%引きで
販売したということが分かります。
図にその情報を書き入れて
整理すると
こういうことになります。
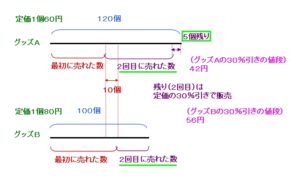
④「グッズAは5個売れ残り、グッズBはすべて売れました。」
定価の30%引きで
販売した結果、
グッズAは5個残ってしまい、
グッズBはすべて売れて
残りは0個ということが分かります。
図で整理してみると
このようになります。
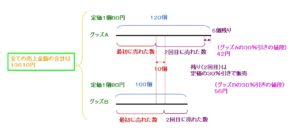
⑤最初に販売したものと、割引後に販売したもののすべての売上金額の合計は、13610円になりました。
そして
始めに定価で販売した
グッズAとグッズBの売上金額と、
その後に
定価の30%引きで販売した
グッズAとグッズBの売上金額の
合計が、
13610円になりました
ということですね。
どうでしょうか?
文章を短く区切って
1つ1つの情報を
図であらわしていくと、
なにが起こっているのか
分かりやすいのではないでしょうか。
ちなみに、
図はこの書き方が
絶対に正解というわけでは
ありません。
文章の内容を
図でしっかりと
あらわすことができていて、
自分が理解しやすいものであれは、
どのように図を描いても
かまいません。
さて、
それでは最後に
⑥最初に定価で販売した時に売れた、グッズAの個数とグッズBの個数を求めなさい。
となっているので、
式を組み立てるための
xとyの情報を
入れていきましょう。
最初に定価で売れたグッズAの個数をx
同じくグッズBの個数をy
としてみます。
※一次方程式や
連立方程式の文章題で、
「xやyを何にするのか」
というのは
とても大切なポイントに
なります。
すべてが
そうなるとは限りませんが、
最初に問題文で
「求めなさい」と
いわれているものを
xやyにすると、
式を組み立てられることが
多いです。
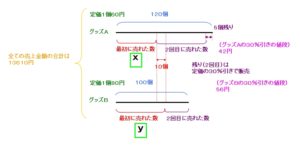
xとyという
2つ分からないものが
出てきたときは、
xとyを含む
2つの異なる式を
作ることができれば、
連立方程式として
xとyを
求めることができましたよね。
図を
ながめてみて下さい。
1つ目の式は、
最初に定価で売れたグッズAの個数(x)と
定価で売れたグッズBの個数(y)の差が
分かりますね。
定価で売れたグッズBの個数(y)の方が
定価で売れたグッズAの個数(x)より
10個多いことが分かります。
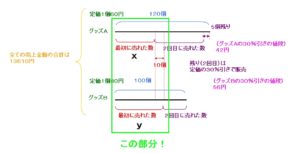
1つ目の式は
x+10=y
になります。
2つ目の式は、
グッズAとグッズBの
全ての売上金額の合計に
注目してみます。
最初の販売については、
グッズA、グッズBともに
定価で売れた数(xとy)、
定価の値段(60円と80円)は
分かっています。
2回目の販売については
グッズA、グッズBともに
割引後の値段(42円と56円)は
分かっています。
あと
2回目の販売で
グッズA、グッズBが
それぞれ何個売れたか
ということが分かれば、
全ての売上金額の合計を
式で表すことができますよね。
グッズAは
2回目の販売の結果
5個売れ残ったので、
2回目の販売の個数は
120-x-5
と表すことができます。
グッズBは
2回目の販売で
すべて売れたので、
2回目の販売の個数は
100-y
と表すことができます。
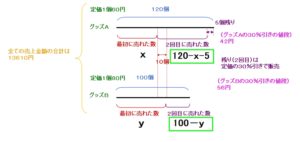
さあ、
これで
グッズAとグッズBの
全ての売上金額の合計を
求めるための材料が
そろいました。
それでは、
一気に
全ての売上金額の合計を
求める式を
組み立ててもかまいませんが、
ここでは
グッズAとグッズBの
売上金額を別々に求めて、
最後に合計するように
していきます。
グッズAの売上金額を
求める式は
次のようになります。

つづいて
グッズBの売上金額を
求める式は
次のようになります

全ての売上金額の合計は
13610円なので、
グッズAとグッズB
それぞれの売上金額を
合計した式は
次のようになります。

これで
xとyを含む
異なる2つの式ができたので、
連立方程式として
xとyを求めていきます。
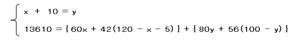
途中式は省略しますが、
この連立方程式を解くと
x=70
y=80
となります。
問題文では
最初に定価で販売した時に売れた、グッズAの個数とグッズBの個数を求めなさい。
といっているので、
答えは
最初に定価で販売した時に売れた
グッズAの個数は70個、
同じくグッズBは80個、
ということになります。
どうでしょうか?
文章題の文が長くて
「わかりずらいな」
と思っても、
書いてある内容を
短く区切って
1つ1つていねいに
整理していけば、
何が起きているのか
理解しやすく
なるのではないでしょうか。
そして最後に
問題が求めている答えを
出すために、
自分が今まで整理したものの中で
どれが使えそうか
ということを考えていけば、
問題を解くための
式を組み立てることが
できるのではないか
と思います。
最初は
時間がかかってしまっても
全然かまわないので、
自分の力で
文章の内容を整理できるように
文章題に取り組んで
みてください。
1つ
自分なりのやり方で整理して、
式を組み立てて
問題を解くことができれば、
コツがつかめてくると思います。
あとは
いろいろな文章題に取り組んで
力をのばしていってください。
まとめ

数学の文章題を解くコツ その2
についてまとめます。
1.文章題に書かれている内容を
一度に理解しようとせずに、
短く区切って
1つ1つていねいに、
内容を整理していく
2.最後に
整理した内容を
つなげて考えて、
答えを求めるために
必要な情報はなにか
(=式を組み立てるのに
どの情報が必要なのか)
を考える
頑張る中学生をかめきち先生は応援しています。
「なんとかしよう」と頑張るあなたなら、
必ずできるようになりますよ!
最後まで読んで頂き、ありがとうございました。