頑張る中学生を応援するかめきち先生です。
今回は、
関数の問題の
小問として
よく出題されることのある
関数のグラフの中にある
三角形の面積を求めるコツ
について
お話をしていきたいと思います。
関数のグラフの中にある
三角形の面積を求める際に、
三角形の中に補助線を引いて
分割して面積を求めるなど
色々な方法があると思いますが、
これからお話をする
コツを使えば、
三角形の頂点である
3つの点の座標が分かれば
どのような形の三角形であっても
面積を求めることができます。
ぜひ
マスターしておきましょう!
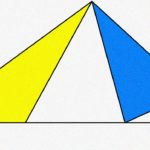
三角形の面積を求めやすいパターン
次の関数のグラフの図で、
△AOBの面積を
求める場合は、
どのようにすれば
よいと思いますか?
(図には表記していませんが、
3点A、B、Cの座標は
分かっているものとします。)

このパターンの場合は、
△AOBを
COを底辺とする
2つの三角形に分割して、
それぞれの面積を求めて
合計する
という方法で
求めることができます。
1つの三角形が
△AOC(次の図の①)
もう1つの三角形が
△BOC(次の図の②)
になります。
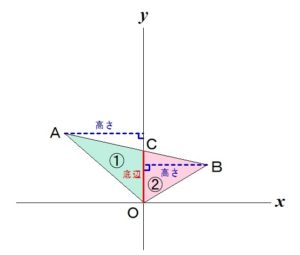
点A、B、Cの
座標の情報から、
それぞれの三角形の
底辺と
高さを
求めることができるので、
△AOC(図の①)と
△BOC(図の②)の
面積を求めて、
それらを合計して
△AOBの面積を
算出することが
できます。
このように
x軸やy軸に平行な線で
三角形を分割して、
底辺と
それぞれの高さを
座標から
求められる場合は、
あまり悩むことなく
面積を求めることが
できると思います。
三角形の面積を求めにくいパターン
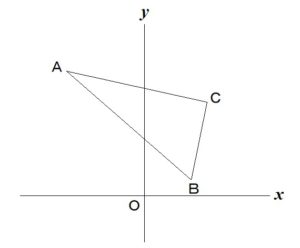
それでは次の図の
△ABCの面積を
求める場合は
どうでしょうか?
(3点A、B、Cの座標は
分かっているものと
します。)
この場合、
三角形の中に
補助線を引くといった
方法でも
面積を求めることは
できますが、
考え方や計算が
複雑になってしまいます。
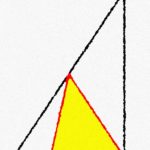
そこで
三角形の頂点である
3つの点(点A、B、C)の座標が
分かるのであれば、
シンプルに三角形の面積を
出せる方法があります。
その方法とは
三角形の頂点である
3つの点(点A、B、C)を通る
長方形(もしくは正方形)を作成して、
そこから
必要ない部分の面積を引いて
三角形の面積を求める
という方法です。
① まず
次の図のように
三角形の頂点である
3つの点(点A、B、C)を通る
長方形を作成します。

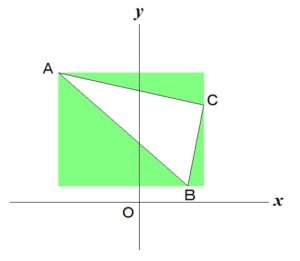
② つづいて
3つの頂点(点A、B、C)の
座標の情報から
長方形の全体の面積を求めて、
そこから
必要のない部分(次の図で緑色の部分)
の面積を引いて
△ABCの面積を
求めていきます。
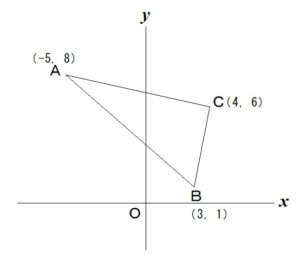
それでは
次の図のように
点A、B、Cの座標の情報が
与えられている場合、
実際に△ABCの面積を
求めてみます。
(自分の力で
できそうであれば、
まずはチャレンジしてみて下さい。)
△ABCの面積の求め方は、
① まず
△ABCの頂点を通る
長方形を作成します。

長方形の横の長さは
Aのx座標が-5
Cのx座標が4
ということから、
5+4=9
ということが分かります。
長方形の縦の長さは
Aのy座標が8
Bのy座標が1
ということから、
8-1=7
ということが分かります。
よって
3点A、B、Cを通る
長方形の面積は、
9×7=63
になります。
② つづいて
必要ない部分の
三角形の面積(緑色の部分)を
求めていきます。
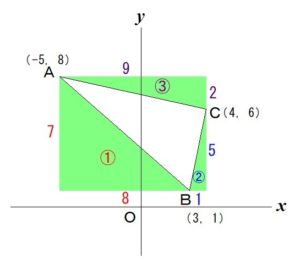
図の①の三角形の底辺は
Aのx座標が-5
Bのx座標が3
ということから、
5+3=8
ということが分かります。
高さは
Aのy座標が8
Bのy座標が1
ということから、
8-1=7
ということが分かります。
同様に
それぞれの座標の情報から、
②の三角形と
③の三角形の
底辺と高さも求めていきます。
次に
図で緑色のついた
それぞれの三角形の面積を
求めていくと、
①の三角形の面積は
8×7×1/2=28
②の三角形の面積は
1×5×1/2=5/2
③の三角形の面積は
9×2×1/2=9
ということになります。
最後に
求めたい△ABCの面積は、
長方形全体の面積から
3つの三角形の面積を
引いたものになるので、
63-28-5/2-9=47/2
ということになります。
以上が
関数のグラフの中にある三角形で
3つの頂点の座標が分かる場合の
三角形の面積の求め方に
なります。
高校入試でも
よく出題されるところなので
しっかりと
マスターしておきましょう!
まとめ

関数のグラフの中にある
三角形の面積を求めるコツ
についてまとめます。
① x軸やy軸に平行な線で
三角形を分割して、
底辺や
それぞれの高さを
座標から容易に
求められるのであれば、
その方法で
三角形の面積を求める。
② ①の方法だと
計算が複雑になりそうな場合は、
三角形の3つの頂点を通る
長方形(もしくは正方形)を作成して、
そこから
必要ない部分の面積を引いて
三角形の面積を求める。
あきらめずにねばり強く取り組めば
必ずできるようになりますよ!
頑張る中学生をかめきち先生は応援しています。
最後まで読んでいただき
ありがとうございました。