頑張る中学生を応援するかめきち先生です。
今回は頑張って数学を勉強しているのに、
模擬試験などでなかなか成績(偏差値)が上がらない
というあなたのために、
かめきち先生が思うところの
成績を上げるコツを伝授します。
「頭の出来がいいから、
成績もいいんでしょ?」
いやいや、そんなことは決してないですよ。
実際にかめきち先生自身の話をすれば
元々の「頭の出来」は
かなり良くない方だと思います。
ここでいう「頭の出来」とは、
難しい問題の解法を
ひらめきで思いついたりする
裏付けをきちんと説明できない
すごい力のことです。
そんな力、
かめきち先生は全く持っていないと
断言できます。(^_^;)
なぜなら
かめきち先生が中学生で
高校受験を控えて模擬試験を受け始めた頃、
数学の成績はさっぱりでした。
まぁ、ひどいものでした。
偏差値50がかすんで見えるくらい
遠いかなた・・。
でも高校受験前には、
偏差値60以上を毎回キープできるまで
成績を伸ばすことができました。
なぜなら
当時ははっきりと認識できていませんでしたが、
今思えば
数学の難しい問題に挑む際に、
あるコツをつかんでいたからです。
そして
これはかめきち先生自身だけの話ではなく、
かめきち先生の多くの生徒も
そのコツをつかんで
同じように高校受験前までに
数学の成績を「ぐんっ」と上げることに
成功しています。
ぞのコツについて
お話していきます。
※今回の話は
現在、偏差値が50を超えていて
なかなか60以上に上げられない、
という人向けの話になります。
「偏差値50に届いていない」という人は、
教科書や問題集の基礎問題に
繰り返し取り組んで、
基礎力をしっかりと身につけましょう。
基礎問題を解答を見ないで
自力で解けるようになれば、
「偏差値50」を突破できます!
数学の成績(偏差値)を上げるコツとは?
数学の成績(偏差値)を上げるためには、
まずしっかりと勉強に取り組んでいること
という大前提があります。
勉強の量が少ないのに
成績(偏差値)が上がっていく
ということはまずないです。
頑張って数学の勉強に取り組んでいるのに
超えられない壁があって、
成績(偏差値)がなかなか上がらない
という人に向けての話になります。
さて
数学の成績(偏差値)を
上げるためのコツとは何なのか、
それはズバリ
難しい問題(応用問題)を解く際に
よく使う解法パターン(考え方)を
身につける
ということです。
解法パターン(考え方)を
身につけるといっても、
よく出題される
代表的な応用問題全てについて、
最初から最後まで全ての解き方を
覚えるということではありません。
問題を解く際の
一番キーとなる部分の考え方
を数多く身につけるということです。
例えば
図のような問題が出題されたとします。
※大きな図形の中に、
この様な図形が組み込まれて
出題されることが多いです。
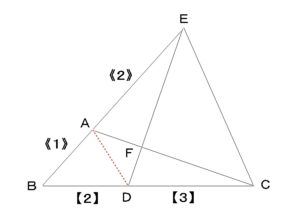
△ADEと△ADCの面積比を求めなさい。
普通に問題に取り組もうとすると
△ADEと△ADCを比べようとしますが、
できませんよね。
そこで
このような問題でよく使われる
解法パターンとして、
「そのまま比べられない図形は
その図形を含んだもう一つ大きな図形で
考えてみる」
という考え方があります。
その視点で見てみると
△ADEは△BDEに含まれ、
△ADCは△ABCに含まれています。
では
△BDEと△ABCで考えてみると、
両方とも共通の部分として
△ABDが含まれています。
△ADEも△ADCも
△ABDと頂点を一緒にする三角形なので、
底辺の比から
それぞれ△ABDの何倍かということが
分かりますよね。
△ADE = △ABD × 2
△ADC = △ABD × 3/2
△ADE : △ADC = △ABD × 2 : △ABD × 3/2
だから、
△ADEと△ADCの面積比は 4 : 3
ということになります。
この例のように、
応用問題に取り組む際に
問題を解くためにキーとなる考え方があり、
受験問題や模擬試験で出題されるものにおいては
それがパターン化されていることが多い
ということが言えます。
ということは
よく使う解法パターン(考え方)を
数多く身につけておけば、
試験で対応できる応用問題が増えて
点数がUPし、
成績(偏差値)が上がるということに
つながりますよね。
どのようにすれば、解法パターンを身につけられる?
それでは
どのようにすれば、
よく使う解法パターン(考え方)を
身につけることができるのでしょうか?
これについては
残念ながら近道はありません。
多くの難しい問題(応用問題)に取り組んで
その中で解法パターンを身につけていく
ということになります。
ただし
ただ単に数多くの問題に取り組む
ということではなく、
「キーとなるポイント(解法)はどこか」
ということを常に意識しながら
問題を解くようにします。
そうすることで
出てきた解法が
記憶に残りやすくなります。
また
同分野の問題に
連続して取り組むということも、
学んだ解法を
記憶に植え付ける方法として
とても効果的です。
例えば
1次・2次関数の複合問題や、
平面図形、空間図形、連立方程式の文章題など、
連続して同分野の問題に取り組みます。
同分野の問題であれば
当然同じ解法パターンを
使用する問題に当たる可能性も
高くなるので、
繰り返し学習効果として
解法パターンが記憶に残るということが
期待できます。
新たな問題に取り組んで、
意識して前に出てきた解法を使って
解くことができたのであれば、
しっかりとそのパターンの解法は
マスターできているという証拠です。
もし問題が解けなかったとしても、
以前使ったことのある解法が
解説に出てきたのであれば、
しっかりとその時点で
マスターするようにしていきましょう。
まとめ

数学の成績(偏差値)を上げるコツについて
まとめます。
1.難しい問題(応用問題)を解く際に
よく使う解法パターン(考え方)を
身につける
2.そのためには
多くの難しい問題(応用問題)に取り組んで
その中で意識して解法パターンを身につけていく
3.同分野の問題に連続して取り組む勉強法は
解法パターンを記憶に残す方法として効果的
最後まであきらめないで自分の力を信じよう!
頑張る中学生をかめきち先生は応援しています。
最後まで読んで頂きありがとうございます。