頑張る中学生を応援するかめきち先生です。
テストで連立方程式の計算問題が出題されました。
「連立方程式の解き方はマスターしているので大丈夫!」
計算を行って答え合わせをしてみると、
「あれ、間違ってる。」
模擬試験の時であれば次にミスしないように
気をつけて計算を行えばよいですが、
本番(定期テストや高校受験)で
これをやっては絶対にいけませんよ。
解き方は分かっていても
部分点がもらえる訳ではないので、
計算ミスで間違えてしまえば
その問題の得点はゼロです。
もったいないです。
本番(定期テストや高校受験)では
普段自分が行っていることが
そのまま出てしまいます。
連立方程式の計算は
ちょっとしたコツで
計算ミスを減らすことができます。
今回は
連立方程式で計算ミスをしないための
コツについてお話していきます。
計算ミスを引き起こす原因は?
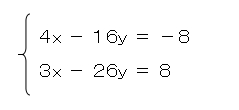
この様な問題が出題されました。
あなたなら、どのように解きますか?
2つの式からxかyのどちらかを
消してあげればよいので、
通常であればxを消すように
計算を行っていくと思います。
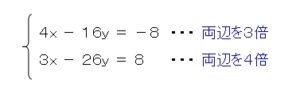
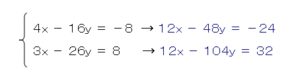
このようにxを消すために
2つの式のxの係数が12になるように、
計算を行っていきます。
さて、次の段階ではあなたなら
どのように計算していきますか?
「2つの式の引き算を行って、
xを消せばいいんじゃないの?」
正解です。
正解なんですが、
実はここに計算ミスを
引き起こしやすくする原因が
潜んでいます。
それは、引き算を行って計算をする
というところです。
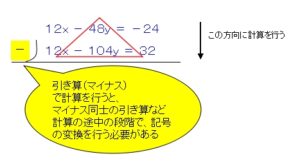
引き算を使って計算を行うと
計算の途中の段階で、
引く側の式(12x-104y=32)
の符号の変換を行う必要が出てきます。
頭の中でこの符号の変換を行ったうえで
計算をする時に、
ミスが起きやすくなります。
符号を変換したことを
一時的に記憶しながら計算を行うので、
計算がシンプルではなくなるからです。
では、
どのように計算を行えば
ミスを防ぐことができるのでしょうか。
ミスを防ぐポイントは足し算!
ポイントは、2つの式を用いて
xかyを消す計算を行う際に、
引き算は使わずに
常に足し算で計算を行うということです。
最初から足し算で
xかyを消すことができる場合はよいのですが、
例題のように
そのまま計算を進めていくと
引き算を使わなければならない場合は、
ひと手間かけてあげる必要があります。

例題の場合だと上記のように
片方の式の両辺に-1をかけて、
符号を逆転させます。
※片方の式の両辺の符号を
すべて逆転する
と覚えておくとよいですよ。
※上記の例では
下の式の符号を逆転させてますが、
当然下の式ではなく
上の式の符号を逆転させてもOKです。
そして
2つの式の足し算を行って
xかyどちらかを消していきます。

足し算で計算をおこなうと、
計算の途中で符号の変換を気にせずに
そのまま符号の通り計算を行えばよいので、
計算がとてもシンプルになります。
計算がシンプルということは、
ミスをしにくくなるということです。
最初は「ひと手間かけるのは面倒だよ」と
思うかもしれませんが、
片方の式の符号をすべて逆転するだけなので
慣れてしまえば手間と思わなくなりますよ。
やり方は分かっているのに
計算ミスで失点しまうというのは、
本当にもったいないです。
連立方程式の計算ミスを減らすこのコツを
ぜひ使ってみて下さい!
ちなみに例題の答えは、
x=-6
y=-1
です。
まとめ

連立方程式で計算ミスをしないコツについて
まとめます。
1.2つの式からxかyのどちらかを
消す計算を行う時に、引き算は使用しない。
2.そのまま計算を続けていくと
引き算を使用しなければならない場合は、
2つの式のどちらかの記号を全て逆転し
(=両辺に-1をかける)、足し算を使用して
計算を行う。計算はシンプルに!
頑張る中学生をかめきち先生は応援しています。
一生懸命取り組んできたことは、必ずあなたの身になります!
最後まで読んで頂き、ありがとうございました。