頑張る中学生を応援するかめきち先生です。
今回は
作図において
具体的な角度の描き方
のお話をしていきます。
定期テストや高校入試の
作図の問題において、
「30°」や「45°」など
具体的な角度を
描くことができなければならない
という場面が
出てくることがあります。
描くことが求められる
角度の種類は
数種類しかないので、
ここでしっかりと
押さえて、
作図を得意分野に
してしまいましょう!
※今回のお話は、
「角の二等分線」
「垂線」
の描き方を
理解していることが
前提となります。
この記事の中で
もう一度描き方の
説明は行っていますが、
キチンと理解できていない
という人は、
「作図のコツ、3つの基本パターン。」
の記事を
参考にしてみてください。
5種類の角度の作図
ここでは
5種類の角度の作図について
お話をしていきます。
60°
30°
90°
45°
120°
それぞれの
角度の描き方について
説明を行っていきます。
作図は
コンパスと定規しか
使うことができないので、
コンパスと定規で
描ける図形の特徴を
上手く利用して
求められている角度を
描いていく
ということが、
ポイントになります。
60°の角の作図
「60°」と言われたら
ある図形を
思い浮かべることが
できませんか?
そうです。
ここでは
正三角形の作図を
利用して、
60°の角を
描いていきます。
次の図の
線分ABに対して、
60°の角をなす
半直線(始点はA)を
描いてみます。

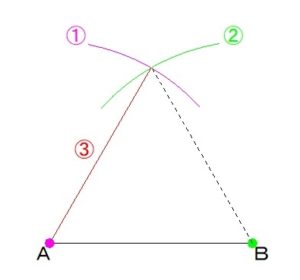
①点Aにコンパスの中心をさし、
点Bにコンパスの開きを合わせて
(=鉛筆の芯を点Bに合わせる)
円を描きます。
②つづいて
点Bにコンパスの中心をさして、
コンパスの開きは
そのままで、
円を描きます。
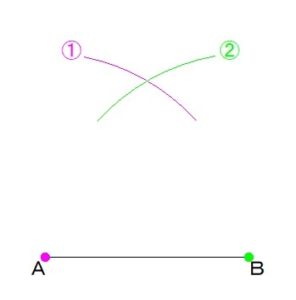
③点Aと円の交点を
線で結びます。
ここでは
実際に線は引きませんが、
点Bから交点まで
線を引くと、
正三角形の図形が
できあがります。
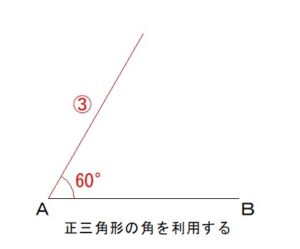
正三角形の1つの角は
60°になるので、
この③の線が
線分ABに対して
60°の角をなす半直線
ということになります。
30°の角の作図
つづいて
30°の角の
作図を行っていきますが、
先ほどの
60°の角の作図を
利用して、
角を描いていきます。
30°は60°の
半分なので、
60°の角の二等分線を
利用して
30°の角を描きます。
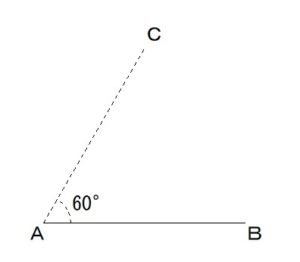
次の図の
線分ABに対して、
30°の角をなす
半直線(始点はA)を
描いてみます。

60°の角を
描くところまでは、
60°の角の作図を
参考にしてください。
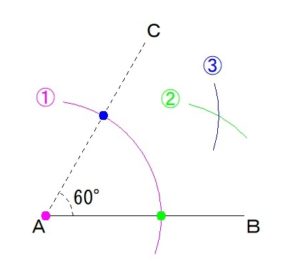
①点Aに
コンパスの中心をさし、
適当な長さに
コンパスを開いて
円を描きます。
(下に図があります)
②つづいて
線分ABと
①で描いた円との交点に
コンパスの中心をさして、
コンパスを適当な長さに開いて
円を描きます。
※コンパスの開きは、
①と同じままでも
大丈夫です。
(下に図があります)
③今度は
線分ACと
①で描いた円との交点に
コンパスの中心をさして、
コンパスの開きは②の長さのまま
円を描きます。
(=②と同じ
半径の円を描く。)
④点Aから
②と③で描いた
円の交点を通る
半直線を引きます。
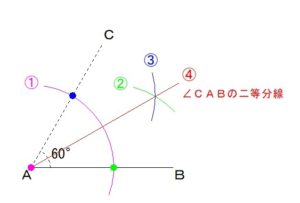
この④の線が
角(∠CAB)の二等分線
ということになります。
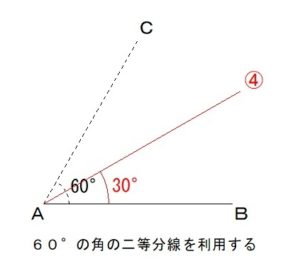
∠CABは60°なので、
この④の線が
線分ABに対して
30°の角をなす半直線
ということになります。
90°の角の作図
90°の角の作図については、
垂線を引くことで
90°の角を描いていきます。
次の図の
線分ABに対して、
90°の角をなす
半直線(始点はO)を
描いてみます。
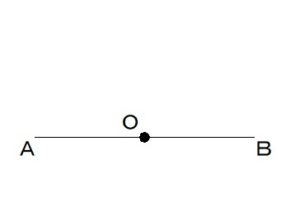
①点Oに
コンパスの中心をさして、
コンパスを適当な長さに開いて
円を描きます。
(線分ABと円との交点が
2つできます。
下に図があります。)
②つづいて
線分ABと
円との2つの交点のうち、
1つ(点C)に
コンパスの中心をさして、
コンパスを適当な長さに開いて
円を描きます。
※コンパスの開きは、
①と同じままでも
大丈夫です。
(下に図があります。)
③今度は
もう片方の交点(点D)に
コンパスの中心をさして、
コンパスの開きは②の長さのまま
円を描きます。
(=②と同じ
半径の円を描く。)
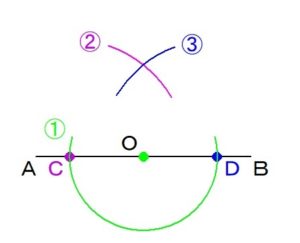
④最後に点Oから
②と③で描いた
円の交点を通る
直線を引きます。
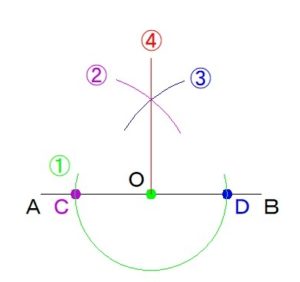
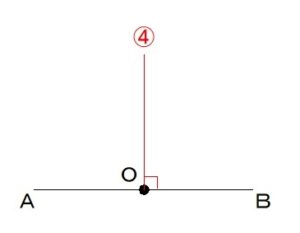
この④の線が
線分ABに対して
90°の角をなす
点Oを始点とする半直線
ということになります。
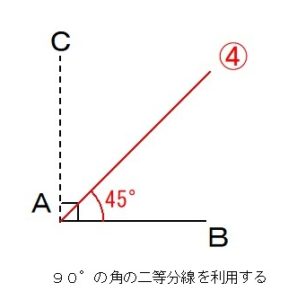
45°の角の作図
45°の角の作図は
30°の時と同様に
90°の半分の角度になるので,
90°の角の二等分線を
利用して
45°の角を描いていきます。
次の図の
線分ABに対して、
45°の角をなす
半直線(始点はA)を
描いてみます。

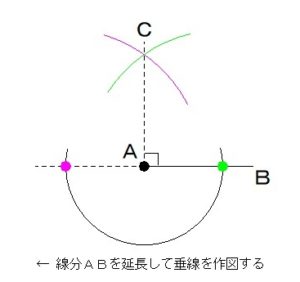
まず点Aを通る
垂線を引いていきますが
そのままでは
描くことが難しいので、
線分ABを延長して
垂線を描いていきます。
(垂線の描き方は
90°の角の作図
を参照)
つづいて
90°の角の二等分線を
描いていきます。
①点Aに
コンパスの中心をさし、
適当な長さに
コンパスを開いて
円を描きます。
(下に図があります)
②つづいて
線分ABと
①で描いた円との交点に
コンパスの中心をさして、
コンパスを適当な長さに開いて
円を描きます。
※コンパスの開きは、
①と同じままでも
大丈夫です。
(下に図があります)
③今度は
線分ACと
①で描いた円との交点に
コンパスの中心をさして、
コンパスの開きは②の長さのまま
円を描きます。
(=②と同じ
半径の円を描く。)
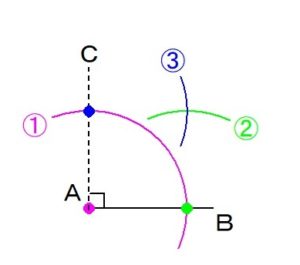
④点Aから
②と③で描いた
円の交点を通る
半直線を引きます。
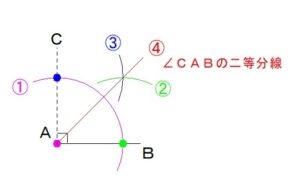
この④の線が
角(∠CAB)の二等分線
ということになります。
∠CABは90°なので、
この④の線が
線分ABに対して
45°の角をなす半直線
ということになります。
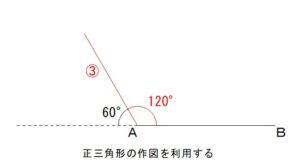
120°の角の作図
それでは最後に
120°の角の作図についてです。
120°は
180°から60°を
ひいたものと、
言いかえることができます。
ということは、
60°の角の作図
(=正三角形を利用した作図)
を利用して、
120°の角を描くことが
できます。
次の図の
線分ABに対して、
120°の角をなす
半直線(始点はA)を
描いてみます。

頂点の1つをAとする
正三角形を描いていきますが、
そのままでは
描くことが難しいので、
線分ABを延長して、
適当な長さのところを
点Cとします。

①点Cにコンパスの中心をさし、
点Aにコンパスの開きを合わせて
(=鉛筆の芯を点Aに合わせる)
円を描きます。
(下に図があります)
②つづいて
点Aにコンパスの中心をさして、
コンパスの開きは
そのままで、
円を描きます。
(下に図があります)
③点Aと円の交点を
線で結びます。

ここでは
実際に線は引きませんが、
点Cから交点まで
線を引くと、
正三角形の図形となります。
この③の線が
線分ACに対しては
60°の角をなす半直線
になります。
ということは
③の線は
逆側の線分ABに対して
120°の角をなす半直線
になるということになります。
以上
5種類の角度の作図について
お話をしてきましたが、
そのほかにも
75°(30°+45°)や
150°(180°-30°)などの
角度の作図が
出題されることがありますが、
これまで学習した
角度の作図の組み合わせで
対応することができます。
5種類の角度の作図を
しっかりと
マスターしておきましょう!
まとめ

角の作図について
まとめます。
1.60°の角の作図は、
正三角形の作図を利用する
2.30°の作図は、
60°の角の二等分線を
利用する
3.90°の作図は、
垂線を利用する
4.45°の作図は、
90°の角の二等分線を
利用する
5.120°の作図は、
60°の角の作図
(180°-60°)を
利用する
6.その他の
角度の作図は、
今までの角の作図の
組み合わせで
対応する
ねばり強く
最後まであきらめずに頑張れば、
必ず成果は
目に見える形となって出てきますよ!
頑張る中学生を
かめきち先生は応援しています。
最後まで読んでいただき
ありがとうございました。